Economic Dispatch¶
ED tries to allocate available generation to meet the current system load at lowest cost. The classic text is Wood & Wollenburg.
The problem¶
\(\min \sum_g C_g(P_g)\)
\(\mathrm{s.t.} P_{\min (g)} \leq P_g \leq P_{\max (g)} \forall \mathrm{generators} (g)\)
\(\mathrm{s.t.} \sum_g P_{g}= P_{\mathrm{load}}\)
In this mathematical formulation generators are indexed by \(g\). \(P_g\) is a generator’s power output and \(C_g()\) is its cost function. The objective is to minimize the total cost. There are two constraints:
each generator must be within its real power limits and
total power generated must equal the power consumed by the load.
Example Problem¶
To define a simple ED problem, Minpower requires two spreadsheets. The first describes the generator parameters (generators.csv):
heat rate equation,P min,P max,fuel cost
225+8.4P+0.0025P^2,45,450,0.8
729+6.3P+0.0081P^2,45,350,1.02
400+7.5P+0.0025P^2,47.5,450,0.9
The second simply describes the load (loads.csv):
name,power
load,500
Note
For more information about what options you can specify in each spreadsheet see: Creating a Problem.
Solving¶
Save the two spreadsheets above into into a folder (call it mydispatch) and run:
minpower mydispatch
This particular problem is also Minpower built-in test case (based on Wood & Wollenburg Problem 3.7), so if you haven’t been following along, to solve it, call:
minpower ed-WW-3-7
Example Solution¶
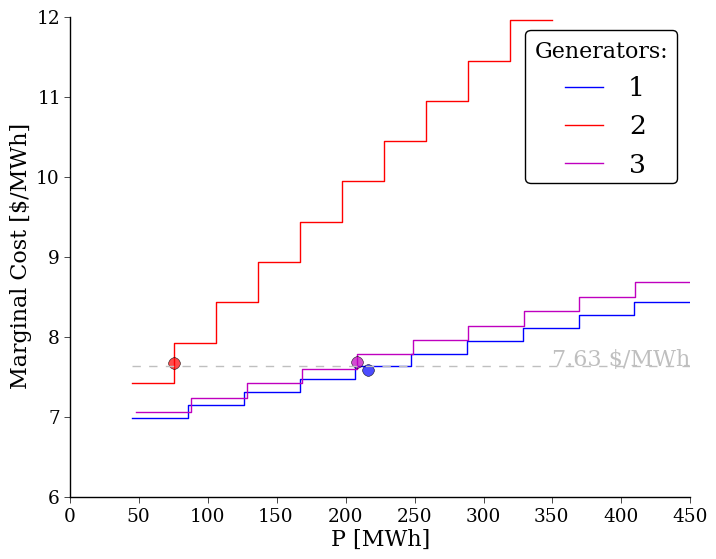
The result is a plot (dispatch.png):
and a spreadsheet (dispatch.csv):
name,power,IC 1,216.000000000001,7.584000000000005 2,75.4999999999998,7.673561999999997 3,208.499999999999,7.688249999999996
These outputs show that the problem’s two generators (named cheap and expensive) are being
dispatched so that their incremental costs (the vertical axis in the plot and IC in the spreadsheet) are near equal.
Each generator’s linearized incremental cost is shown in the plot, with a dot on its current real power output (P).
Because this is a dispatch each generator is on (u=True) unless specified in the input spreadsheet.